[컴퓨터 구조]Chapter 2. Instructions : Language of the Computer

[ MIPS R-format Instruction ]

op	rs	rt	rd	shamt	funct
6bits	5 bits	5 bits	5 bits	5 bits	6bits

각 필드 명칭

op : operation code(opcode)

rs : first source register number

rt : second source register number

rd : destination register number

shamt : shift amount

funct : function code (extends opcode)

[ MIPS I-format Instruction ]

op	rs	rt	constant or address
6 bits	5 bits	5 bits	16 bits

사용되는 명령어 : Immediate arithmetic, load/store Instruction에 사용된다.

이는 MIPS의 원칙 Make the common case fact를 위해서이다. small constants are common, Immediate operand avoids a load instruction(상수 연산은 흔한데, 상수 연산을 할 때마다 메모리에서 상수를 가져오는 lw연산을 피할 수 있으므로 연산을 매우 빠르게 할 수 있다.)

No subtract immediate instruction. Just use a negative constant.(상수 빼기 연산은 존재하지 않는다. 단지 음수 상수를 더하면 된다.)

각 필드 용도

rt :

Constant : -2^15 ~ 2^15 -1

Address : offset added to base address in ra

상수 0 : MIPS 레지스터의 0번째 레지스터인 $zero는 상수 이다. 이를 overwritten을 할 수 없다. 이 명령을 가지고 MIPS에 없는 move 명령을 할 수 있다.

예] add $t2, $s1, $zero은 $s1에 저장된 값을 $t2로 보내는 역활을 한다.

[ MIPS Memory Operand ]

MIPS는 빅엔디안(Big Endian) 방식이다.(시작 주소에 상위 바이트 부터 기록하는 방식)

[예제] 다음과 같은 C코드가 있다.

A[12] = h + A[8];

h는 $s2, A의 베이스 주소는 $s3에 있다. 이의 MIPS 코드를 자성하라.

[답]

lw $t0, 32($t3)

add $t0, $s2, $t0o

sw $t0, 48($s3)

[ SHIFT operations ]

sll은 i 만큼 2^i 만큼 곱한 것이다.

srl은 i 만큼 2^i 만큼 나눈 것이다.

sll $t2,$s0, 4

op

rs

rt

rd

shmant

funct

0

0

16

10

4

0

[ AND operations ]

Select some bits, clear others to 0. (선택된 비트는 변하지 않고, 선택하지 않는 비트는 0으로 바꾼다.)

[예제] and $t0, $t1, $t2

$t2 0000 0000 0000 0000 0000 1101 1100 0000

$t1 0000 0000 0000 0000 0011 1100 0000 0000

$t0 0000 0000 0000 0000 0000 1100 0000 0000

$t1이 1인 비트를 $t2 값을 가져온다고 생각하면 된다.

[ OR operations ]

Set some bits to 1, leave others unchanged.(정해진 비트를 1로 맞추고 나머지들은 수정하지 않는다.)

[예제] or $t0, $t1, $t2

$t2 0000 0000 0000 0000 0000 1101 1100 0000

$t1 0000 0000 0000 0000 0011 1100 0000 0000

$t0 0000 0000 00000 0000 0011 1101 1100 0000

$1의 비트가 1인 부분에 $t2의 비트가 1로 변한다. 나머지 $2의 비트는 $t0로 간다.

[ Not operations ]

각 워드들을 invert bits하기 위해여 사용한다. 0이라면 1로 1이라면 0으로 바꾼다. MIPS에서는 not 연산이 따로 존재하지 않고 NOR연산과 $zero operand를 사요하여 not연산을 한다. NOR은 둘 다 거짓일 때 참이 나온다. 따라서 0이라면 1로, 1이라면 0으로 바꿀 수 있는 것이다.

MIPS 명령어 : nor $t0, $t1, $zero

[예제]

$t1에 0000 0000 0000 0000 0011 1100 0000 0000이 있다. 이를 not을 수행하여 $t0에 저장하라.

nor $t0, $t1, $zero를 하면

$t0은 1111 1111 1111 1111 1100 0011 1111 1111로 된다.

[ Branch operations ]

- beq rs, rt, L1

rs와 rt의 값이 같으면 labeled L1으로 간다.

- bne rs, rt, L1

rs와 rt의 값이 다르면 labeled L1으로 간다.

- j L1

조건없이 이 문장을 만나면 labeled L1으로 간다.

[C code]

if (i == j) f = g + h;

else f = g - h;

이 C code를 MIPS 명령어로 바꾸어라. (f, g, h, i, j in $s0, $s1, $s2, $s3, $s4)

bne

$s3

$s4

Else

add

$s0

$s1

$s2

j

Exit

Else:

sub

$s0

$s1

$s2

Exit:

...

[ Set on Less than ]

- slt rd, rs, rt

if (rs < rt) rd = 1; else rd = 0;

- slti rt, rs, constant

if (rs < constant) rt = 1; else rt = 0;

- 이 명령어는 beq, bne와 함꼐 사용한다.

slt

$t0,

$s1,

$s2

bne

$t0,

$zero,

- 왜 blt, bge 명령어가 MIPS에는 없을까? 이는 $zero에 있는 상수 0을 이욜해서 모든 조건을 만들 수 있다. 또한 Good design demands good compromise라는 원칙을 준수하여 하드웨어는 간단해야 한다는 von Neumann의 경고를 준수하였다. 구현하기 너무 복잡한 blt명령어들을 제외한 것이다.

[ Logical operations ]

[ Byte/Half word operations ]

[ 2진수 / 16진수 Machine language 읽어서 MIPS 명령어로 전환하기 ]

[문제] 다음과 같은 2진수 32 bits가 있다. 이에 해당하는 MIPS 명령어로 전환하라.

000000 10001 10010 01000 00000 100000 (앞의 수는 2진수이다.)

[해설]

주어진 비트의 앞의 6 bits와 뒤의 6 bits를 읽어서 어떤 명령어의 형태인지 확인한다. 앞의 6 bits가 000000 이므로 주어진 명령어 form은 R-format이다. funct포멧이 100000이므로 이는 add 연산에 해당한다.

op	rs	rt	rd	shamt	funct
6bits	5 bits	5 bits	5 bits	5 bits	6bits

000000

10001

10010

01000

00000

100000

op 000000은 R-format이다. funct 100000는 add 명령어를 사용하겠다.

rs의 10001은 10진수 17 => $s1

rt의 10010은 10진수 18 => $s2

rd의 01000은 10진수 8 => $t0

shamt : 00000은 0, 즉 shift를 하지 않는다.

[예제] 다음과 같은 MIPS 명령어가 있다.

lw $t0, 1200($t1)

add $t0, $s2, $t0

sw $t0, 12000(t1)

이를 기계어로 변환하라.

lw $t0, 1200($t1) # Temporart reg $t0 gets A[300]

add $t0, $s2, $t0 # Temporary reg $t0 gets h + A[300]

sw $t0, 12000(t1) # Stores h + A[300] back into A[300]

Address/shamt

Funct

1200

위 표의 10진수 표현을 2진수로 변환한 값은 다음과 같다.

Address/shamt

Funct

100011

01001

01000

0000 0100 1011 0000

000000

10010

01000

00000

1000000

101011

01001

01000

0000 0100 1011 0000

[ Memory Layout ]

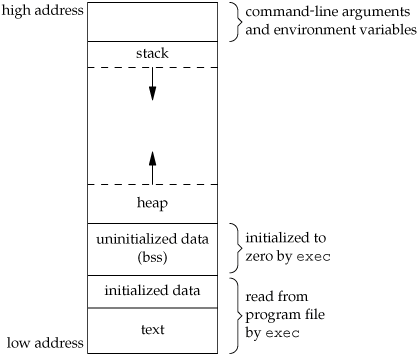
( 이미지 출처 : http://www.geeksforgeeks.org/memory-layout-of-c-program/ )

Text : program code

Static data(그림에서 uninitialized data + initialized data 부분을 합쳐 놓은 곳) : global variables

C에서 static 변수의 값은 $gp가 이 값의 중간값을 가지고 있다.

Dynamic data : heap영역, malloc()으로 공간이 확장되고, free()로 매모리를 헤제한다. 이 영역에 해당함.

Stack : automatic storage

* memory leak(메모리 누수) : Forgetting to free space lead to memory leak.(매모리 공간을 free하는 것을 잊어버리면 메모리 누수가 발생한다.)

* dangling pointer(매달린 포인터) : pointers to point to things that the program never intended.(프로그램이 의도하지 않은 곳에 포인터가 지칭하는 것을 말한다.)

[ MIPS Design Principle ]

다음과 같이 설계 원칙을 따른다.

Design Principle 1 : Simplicity favors Regularity

Design Principle 2 : Smaller is Faster

Design Principle 3 : Make the Common Case Fast

Design Principle 4 : Good Design demands good Compromise

하나씩 설명을 하겠다.

Design Principle 1 : Simplicity favors Regularity

- 모든 명령의 길이를 똑같이 함

- 산술 명령어는 항상 레지스터 피연산자가 세 개를 갖게 한다.

- 어떤 명령어 형식에서나 레지스터 필드의 위치가 일정하게 만든다.

- 규칙성은 인스트럭션을 간단하게 한다.

- 규칙적이면 저비용으로 높은 성능을 낼 수 있다.

Design Principle 2 : Smaller is Faster

- 레지서터의 수가 많아지면 속도가 빨라지는게 아니라 전기 신로를 멀리 보내야 하기 때문에 clock cycle time이 증가한다.

Design Principle 3 : Make the Common Case Fast.

- 상수 같이 자주 사용하는 것들은(산술 연산에서 50%를 차지한다. ) 일일이 lw를 사용하여 상수를 불러오는 것이 아니라 상수형을 만든다.

Design Principle 4 : Good Design demands good Compromise

- 명령어 내부의 주소나 상수부는 클 수록 좋다는 것과, 모든 명령어의 길이는 같다는 것이 좋다는 두 요구사항을 절충한다.

- Different formats complicated decoding, but allow 32-bit instructions uniformly.(다른 포멧들은 디코딩하는데 복잡한다. 그러나 32 비트로)

- Keep format as similar as possible.

[ Addressing Modes. ]

다양한 Addressing Mode가 존재한다. 이를 통해서 인스트럭션의 주소 필드 비트 수를 줄이게 한다.

Effective Address (E.A.) : EA에 저장된 값(주소)를 가지고 메모리에 접근하면 그 자리에 operand가 있다.

1. Implied addressing mode

- Explicit address는 없다. 암묵적으로 약속되어 있는 방식으로 이동한다.

- 예] RTS (Return From Subroutine) 에서

PUSH A

ADD A 의 명령어를 실행하면 AC와 A의 합이 수행된다.

2. Immediate addressing mode

- Operand field contains the actual operand value( Operand 필드가 실제 operand 값을 가지고 있다. 즉 Operand가 명령어 안에 있는 것이다. )

3. Register addressing mode

- Selected Register contains the operand( 명령어에 필드에 있는 상수가 레지스터의 번호이다. )

- E.A. : 명령어 필드에 있는 레지스터 번호

4. Register Indirect addressing mode

- Selected register contains the address of operands(명령어 필드에 있는 상수가 레지스터의 번호이다. 이 레지스터에 주소가 저장되어 있는데 이것이 operand의 주소이다.)

- E.A. : contents of selected register

5. Direct addressing mode

- Effective address is equal to the address part of the instruction and operands reside in memory (유효 주소는 명령어 주소 부분과 동일하며 피연산자는 메모리에 있다.)

- E.A. = Address Field of Instruction

6. Indirect addressing mode

- The address field give the address where the effective address is stored. (주소필드는 실제 주소가 어디에 있는지 알려준다.)

- E.A. = Memory[Address Field of Instruction]

7. (PC) Relative addressing mode

- Value in PC is addend to the address part of instruction to obtain the effective address (PC와 인스트럭션의 주소 부분의 오프셋의 합이이다. - 브렌치 형이 이에 속한다.)

- E.A. = PC + Offset in Address Field of Instruction

8. Indexed addressing mode

- Value in Index Register(offset) is added to the address part of instruction (base address) to obtain the effective address.

- E.A. = Index Register + the Address Field ()B

9. Base register addressing mode

- Value in Base Register(base address) is added to the address part of instruction (offset) to obtain the effective address (to facilitate the relocation of programs in memory)

- E.A. = Base Register + Offset in the Address Field of Instruction

[예제]

Q. 각각의 Address mode에 대해서 Effective address와 Operand Value를 구하라. ( LD의 인스트럭션은 주소 0 에 있다고 가정하라)

Address mode	EA	Content of AC
Direct	5	10
Immediate	0	5
Indirect	10	20
Relative	PC of next instruction 1 + 5 = 6	12
Indexed	5(Base Register) + Index Register = 8	12
Register	?	9
Register indirect	9	25

Q. 각각의 Address mode에 대해서 Effective address와 Operand Value를 구하라.

[답]

Address mode	EA	Content of AC
Direct	500	800
Immediate	201	500
Indirect	800	300
Relative	202+500*1	325
Indexed	500+100 = 600	900
Register	Reg 400번	400
Register indirect	400	700

*주의 Relative의 EA를 구할 때 본 명령어는 MIPS명령어와 다르게 한 주소와 다른 주소의 차이가 1씩 난다. 따라서 offset은 1이 된다.

[첨부]

Figure1. MIPS에서 각 레지스터 번호의 의미

[ Problem Solving ]

해설 문제 : 17, 26

2.17 [5] <§2.5> Provide the type, assembly language instruction, and binary representation of instruction described by the following MIPS fields:

( 다음 MIPS 필드에 설명 된 [1]명령어의 종류, [2]어셈블리 언어 명령어, [3]명령어의 이진 표현을 나타내라. )

opcode

(6 bits)

(5 bits)

immediate

(16 bits)

100011

00001

00010

0000 0000 0000 0100

답>

[1]i-type [2] lw $v0, 4($at)

[3]100011 00001 00010 0000000000000100

2.26 Consider the following MIPS loop:

LOOP: slt $t2, $0, $t1

beq $t2, $0, DONE

subi $t1, $t1, 1

addi $s2, $s2, 2

j LOOP

DONE:

2.26.1 [5] <§2.7> Assume that the register $t1 is initialized to the value 10. What is the value in register ＄s2 assuming the ＄s2 is initially zero?

2.26.2 [5] <§2.7> For each of the loops above, write the equivalent C code routine. Assume that the registers ＄s1, ＄s2, ＄t1, and ＄t2 are integers A, B, i, and temp, respectively.

2.26.3 [5] <§2.7> For the loops written in MIPS assembly above, assume that the register ＄t1 is initialized to the value N. How many MIPS instructions are executed?

2.26 다음 MIPS 순환문을 생각해 보자.

2.26.1 레지스터 $t1은 10으로 초기화 되어있다고 가정하자. $s2가 처음에 0이었다면 레지스터 $s2의 값은 무엇이겠는가?

2.26.2 위 순환문에 해당하는 C코드 루틴을 작성하라.

다음과 같이 가정한다. $s1, $s2, $t1, $t2는 각각 정수 A, B, i, temp이다.

2.26.3 위에서 작성된 루프 MIPS 어셈블리언어에서 레지스터 $t1이 N으로 초기화

된다면 얼마나 많은 MIPS 명령어가 실행될 것인가?

MIPS 각 단계에 대한 해석

LOOP:	slt	$t2, $0, $t1	#$0 < $t1일 때 $t2 = 1이다.
	beq	$t2, $0, DONE	# $t2 == $0이라면 DONE으로 간다.
	subi	$t1, $t1, 1	# $t1에 $t1의 값의 –1한 값을 넣는다.
	addi	$s2, $s2, 2	# $s2에 $s2의 값의 +2한 값을 넣는다.
	j	LOOP
DONE:

2.26.1 sol> $t1은 10으로 초기화, $2가 처음에 0이었을 떄 $s2의 값을 찾는 것이다.

[1 실행]

LOOP:	slt	$t2, $0, $t1	# 0 < 10; 즉, $t2 = 1
	beq	$t2, $0, DONE	# 1 != 0; 이므로 바로 다음 명령어 실행
	subi	$t1, $t1, 1	# $t1 = 10 - 1= 9
<	addi	$s2, $s2, 2	# $s2 = 0 + 2= 2
	j	LOOP	# LOOP로 점프한다.
DONE:

[1 실행]의 $s2는 2이다.

[2 실행]

LOOP:	slt	$t2, $0, $t1	# 0 < 9; 즉, $t2 = 1
	beq	$t2, $0, DONE	# 1 != 0; 이므로 바로 다음 명령어 실행
	subi	$t1, $t1, 1	# $t1 = 9 - 1= 8
	addi	$s2, $s2, 2	# $s2 = $s2 + 2= 4
	j	LOOP	# 다시 반복 시작
DONE:

[2 실행]의 $s2는 4이다.

[3 실행]

LOOP:	slt	$t2, $0, $t1	# 0 < 8; 즉, $t2 = 1
	beq	$t2, $0, DONE	# 1 != 0; 이므로 바로 다음 명령어 실행
	subi	$t1, $t1, 1	# $t1 = 8 - 1= 7
	addi	$s2, $s2, 2	# $s2 = $s2 + 2= 6
	j	LOOP	# 다시 반복 시작
DONE:

[3 실행]의 $s2는 6이다.

[4 실행]

LOOP:	slt	$t2, $0, $t1	# 0 < 7; 즉, $t2 = 1
	beq	$t2, $0, DONE	# 1 != 0; 이므로 바로 다음 명령어 실행
	subi	$t1, $t1, 1	# $t1 = 7 - 1= 6
	addi	$s2, $s2, 2	# $s2 = $s2 + 2= 8
	j	LOOP	# 다시 반복 시작
DONE:

[4 실행]의 $s2는 8이다.

[5 실행]

LOOP:	slt	$t2, $0, $t1	# 0 < 6; 즉, $t2 = 1
	beq	$t2, $0, DONE	# 1 != 0; 이므로 바로 다음 명령어 실행
	subi	$t1, $t1, 1	# $t1 = 6 - 1= 5
	addi	$s2, $s2, 2	# $s2 = $s2 + 2= 10
	j	LOOP	# 다시 반복 시작
DONE:

[5 실행]의 $s2는 10이다.

[6 실행]

LOOP:	slt	$t2, $0, $t1	# 0 < 5; 즉, $t2 = 1
	beq	$t2, $0, DONE	# 1 != 0; 이므로 바로 다음 명령어 실행
	subi	$t1, $t1, 1	# $t1 = 5 - 1= 4
	addi	$s2, $s2, 2	# $s2 = $s2 + 2= 12
	j	LOOP	# 다시 반복 시작
DONE:

[6 실행]의 $s2는 12이다.

[7 실행]

LOOP:	slt	$t2, $0, $t1	# 0 < 4; 즉, $t2 = 1
	beq	$t2, $0, DONE	# 1 != 0; 이므로 바로 다음 명령어 실행
	subi	$t1, $t1, 1	# $t1 = 4 - 1= 3
	addi	$s2, $s2, 2	# $s2 = $s2 + 2= 14
	j	LOOP	# 다시 반복 시작
DONE:

[7 실행]의 $s2는 14이다.

[8 실행]

LOOP:	slt	$t2, $0, $t1	# 0 < 3; 즉, $t2 = 1
	beq	$t2, $0, DONE	# 1 != 0; 이므로 바로 다음 명령어 실행
	subi	$t1, $t1, 1	# $t1 = 3 - 1= 2
	addi	$s2, $s2, 2	# $s2 = $s2 + 2= 16
	j	LOOP	# 다시 반복 시작
DONE:

[8 실행]의 $s2는 16이다.

[9 실행]

LOOP:	slt	$t2, $0, $t1	# 0 < 2; 즉, $t2 = 1
	beq	$t2, $0, DONE	# 1 != 0; 이므로 바로 다음 명령어 실행
	subi	$t1, $t1, 1	# $t1 = 2 - 1= 1
	addi	$s2, $s2, 2	# $s2 = $s2 + 2= 18
	j	LOOP	# 다시 반복 시작
DONE:

[9 실행]의 $s2는 18이다.

[10 실행]

LOOP:	slt	$t2, $0, $t1	# 0 < 1; 즉, $t2 = 1
	beq	$t2, $0, DONE	# 1 != 0; 이므로 바로 다음 명령어 실행
	subi	$t1, $t1, 1	# $t1 = 1 - 1= 0
	addi	$s2, $s2, 2	# $s2 = $s2 + 2= 20
	j	LOOP	# 다시 반복 시작
DONE:

[10 실행]의 $s2는 20이다.

[11 실행]

LOOP:	slt	$t2, $0, $t1	# 0 < 0; 즉, $t2 = 0
	beq	$t2, $0, DONE	# 0 == 0; 이므로 DONE으로 이동
	subi	$t1, $t1, 1
	addi	$s2, $s2, 2
	j	LOOP
DONE:

레지스터 $s2의 값은 20이다.

...

<><

...

저작자표시

'Computer Science > Computer Architecture' 카테고리의 다른 글

파이썬 코드로 보는 멀티스레드 (9)	2021.04.03
👀 한 눈에 확인하는 컴퓨터 구조 (2)	2019.05.02
CISC / RISC (0)	2018.07.14
[컴퓨터 구조]Chapter 3. Arithmetic for Computers (2)	2017.10.25
[컴퓨터 구조]Chapter 1. Computer Abstractions and Technology (7)	2017.10.24

Covenant

[컴퓨터 구조]Chapter 2. Instructions : Language of the Computer

'Computer Science > Computer Architecture' 카테고리의 다른 글

티스토리툴바